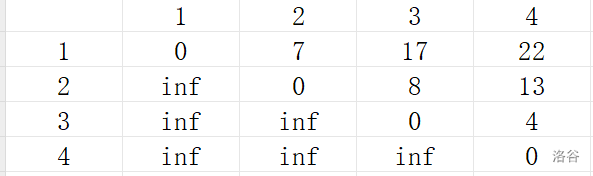区间 dp 笔记

P1775 石子合并（弱化版）

定义 $dp_{i,j}$ 表示合并区间 $[i,j]$ 的石子的最小花费。

我们枚举中间的断点 $k$，$i\le k < j$，转移方程为

$$dp_{i,j}=\min(dp_{i,k},dp_{k+1,j})+sum_j-sum_{i-1}$$

其中 $sum$ 是前缀和。

由于是从一小堆合并到一大堆，所以区间的长度（$j-i+1$）是要从小到大的，所以最外面的循环是从 $2$ 到 $n$ 的（合并长度为 $1$ 的区间代价为 $0$）。

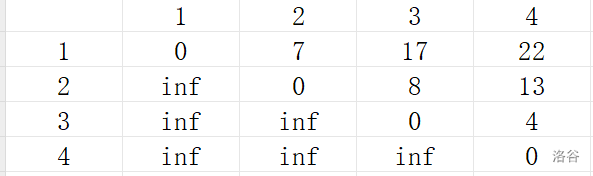
:::align{center}
$\footnotesize \textrm{ 样例的 dp 数组}$
:::

#include<bits/stdc++.h>
using namespace std;
int n,a[305],sum[305],dp[305][305]; 
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)dp[i][j]=1e9;
	for(int i=1;i<=n;i++)cin>>a[i],sum[i]=sum[i-1]+a[i],dp[i][i]=0;
	for(int len=2;len<=n;len++)
		for(int s=1;s<=n-len+1;s++){
			int e=s+len-1;
			for(int j=s;j<e;j++)
				dp[s][e]=min(dp[s][e],dp[s][j]+dp[j+1][e]+sum[e]-sum[s-1]);
		}
	cout<<dp[1][n];
	return 0;
}

P1880 只需要将 $a$ 数组复制一遍粘到后面，然后定义两个 $dp$ 数组就行了。

P1435 [IOI 2000] 回文字串

定义 $dp_{i,j}$ 为使字串 $[i,j]$ 为回文的最小操作次数。

老样子，第一层循环枚举区间长度（因为长的区间是由短的区间得出来的）。

如果 $s_i = s_j$ 那么不用操作 $dp_{i,j}=dp_{i+1,j-1}$。

否则 $dp_{i,j}=\min(dp_{i,j-1},dp_{i+1,j})+1$。

#include<bits/stdc++.h>
using namespace std;
int dp[1005][1005];
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	string s;
	cin>>s;
	int n=s.size();
	s=" "+s;
	for(int len=2;len<=n;len++)
		for(int i=1;i+len-1<=n;i++){
			int j=i+len-1;
			if(s[i]==s[j])len==2?dp[i][j]=0:dp[i][j]=dp[i+1][j-1];
			else dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1;
		}
	cout<<dp[1][n];
	return 0;
}

最长回文字串

额这么板的题在洛谷居然没有。

给定一个字符串 $s$，让你求出最长回文子串的长度。

这题跟上面那题很像，定义状态 $dp_{i,j}$ 表示区间 $[i,j]$ 中的最长回文子串的长度，$vis_{i,j}$ 表示区间 $[i,j]$ 字串是不是回文的，帮助 $dp$ 转移。

首先预处理出长度为 $2$ 的区间，然后 $len$ 从 $3$ 开始枚举。

转移方程：

• 若 $s_i=s_j$ 并且 $vis_{i+1,j-1}=1$，那么 $dp_{i,j}=dp_{i+1,j-1}+2$，更新 $vis_{i,j}=1$

• 否则 $dp_{i,j}=\max({dp_{i+1,j},dp_{i,j-1}})$，$vis_{i,j}=0$

#include<bits/stdc++.h>
using namespace std;
int dp[1005][1005];
bool vis[1005][1005];
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	string s;
	cin>>s;
	int n=s.size();
	s=" "+s;
	for(int i=1;i<=n;i++)dp[i][i]=1,vis[i][i]=1;
	for(int i=1;i<n;i++)
		if(s[i]==s[i+1])dp[i][i+1]=2,vis[i][i+1]=1;
		else dp[i][i+1]=1,vis[i][i+1]=0;
	for(int len=3;len<=n;len++)
		for(int i=1;i+len-1<=n;i++){
			int j=i+len-1;
			if(s[i]==s[j]&&vis[i+1][j-1])dp[i][j]=dp[i+1][j-1]+2,vis[i][j]=1;
			else dp[i][j]=max(dp[i+1][j],dp[i][j-1]),vis[i][j]=0;
		}
	cout<<dp[1][n];
	return 0;
}

话说这题 Manacher 只需要 $O(n)$，但我不会。

CF245H Queries for Number of Palindromes

一道练手好题。

定义 $dp_{i,j}$ 为区间 $[i,j]$ 中的回文字串数，$vis_{i,j}$ 表示区间 $[i,j]$ 是否为回文串。

先处理出长度 $\le3$ 的区间。

for(int i=1;i<=n;i++)dp[i][i]=1,vis[i][i]=1;
	for(int i=1;i<n;i++){
		vis[i][i+1]=s[i]==s[i+1];
		dp[i][i+1]=dp[i][i]+dp[i+1][i+1]+vis[i][i+1];
	}

状态转移方程：$vis_{i,j}=[s_{i}=s_{j}] \land vis_{i+1,j-1}$，$dp_{i,j}=dp_{i+1,j}+dp_{i,j+1}-dp_{i+1,j-1}+vis_{i,j}$。

其中 $[\ ]$ 是艾佛森括号，满足括号内条件返回 $1$ 否则返回 $0$。$\land$ 表示与运算。

#include<bits/stdc++.h>
using namespace std;
int n,m,dp[5005][5005];
bool vis[5005][5005];
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	string s;
	cin>>s;
	n=s.size();
	s=" "+s;
	for(int i=1;i<=n;i++)dp[i][i]=1,vis[i][i]=1;
	for(int i=1;i<n;i++){
		vis[i][i+1]=s[i]==s[i+1];
		dp[i][i+1]=dp[i][i]+dp[i+1][i+1]+vis[i][i+1];
	}
	for(int len=3;len<=n;len++)
		for(int i=1;i+len-1<=n;i++){
			int j=i+len-1;
			vis[i][j]=vis[i+1][j-1]&&s[i]==s[j];
			dp[i][j]=dp[i+1][j]+dp[i][j-1]-dp[i+1][j-1]+vis[i][j];
		}
	cin>>m;
	while(m--){
		int l,r;
		cin>>l>>r;
		cout<<dp[l][r]<<"\n";
	}
	return 0;
}