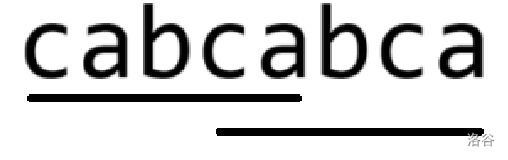KMP 学习笔记

什么是 KMP？

Kill Me Please Knuth Morris Pratt 算法简称 KMP 算法，可以 $O(n+m)$ 的复杂度高效地解决字符串匹配问题。

概念

• $|S|$ 表示字符串 $S$ 的长度。
• 前缀：包含第一个字符的子串。例如 $\texttt {a}$，$\texttt {ab}$，$\texttt{abd}$ 都是 $\texttt{abdabcd}$ 的前缀。
• 后缀：包含最后一个字符的子串。$\texttt{abdabcd}$ 的后缀有 $\texttt d$，$\texttt {cd}$，$\texttt{bcd}$ 等。
• 真前缀：不包含 $S$ 的前缀。真后缀同理。
• border 串：一个子串 $t$ 使得 $t$ 既是 $S$ 的真前缀，又是 $S$ 的真后缀。
• $S_{i \dots j}$ 表示截取 $S$ 的 $[i,j]$ 子串。

border 串的用处

对于待匹配串 $\texttt {abcababac}$，模式串 $\texttt{abab}$。

遍历到 $i=2$ （下标从 0 开始）时发现：

$$\texttt{\color{blue}ab\color{red}{c}\color{black}ababac}\\ \texttt{\color{blue}ab\color{red}a\color{black}b\ \ \ \ \ }$$

失配了，我们将模式串向右移动 2 位，继续匹配。

再举个例子：

待匹配串：$\texttt {abcacababcab}$，模式串 $\texttt{abcab}$。

$$\texttt{\color{blue}abca\color{red}{c}\color{black}ababcab}\\ \texttt{\color{blue}abca\color{red}b \ \ \ \ \ \ }$$

发现 $i=4$ 时失配，将模式串向右移动 3 位对齐，继续匹配。

$$\texttt{abcacababcab}\\ \texttt{abcab\ }$$

对于每一个位置失配，都有一个“向右移动数”。对于例 1 来说，第 2 位失配时，看 0 到 2 位的这个子串，发现 $\texttt a$ 是 0 到 2 这个子串的 border 串。例 2 同理。

在这种前缀后缀相同的情况下，失配前，模式串的后缀验证了可以和待匹配串匹配，那么这个前缀也可以匹配，就不用从头开始重复比较，这就是 KMP 快的地方。

如何快速求出 nxt 数组

我们令 $S_{0\dots i}$ 中最长 border 串长度为 $nxt_i$，模式串的长度为 $n$。

立方级别的算法就不讲了。

当我们已知 $nxt_{i-1}=3$，计算 $nxt_i$ 时，如果发现 $S_i=S_3$，那么可以借助前面的计算得到 $nxt_i=nxt_{i-1}+1$ 的结论。

$$\underbrace{\overbrace{\texttt{abc}}^{nxt_{i-1}}\texttt{d}}_{nxt_i}\dots\underbrace{\overbrace{\texttt{abc}}^{nxt_{i-1}=3}\texttt{d}}_{nxt_i=nxt_{i-1}+1=4}$$

但 $S_i ≠ S_3$ 时，该怎么办呢？枚举更短的 border 并判断相同，然后继续匹配。

枚举更短 border 时，每减少一次 border 的长度，后面必有对应的增加长度的过程，增加的长度不会超过 $n$，故减少的长度也不会超过 $n$，故时间复杂度为 $O(n^2)$。

这个算法依然很慢，慢在枚举更短 border。

这时，K，M，P 三个人站出来了。

枚举更短 border 串可以优化。既然最长的不行，那就找次长的，我们要找的 $S_{0\dots i-1}$ 中次长的 border 串，而 $S_{0\dots 3}=S_{i-4\dots i-1}$，所以 $S_{0\dots i-1}$ 中次长的 border 串就是 $S_{0\dots nxt_{i-1}-1}$ 中的最长 border 串的长度，就是 $nxt_{nxt_{i-1}}$，如果还不行就继续迭代尝试。

因为不用判断子串相同，故时间复杂度为 $O(n)$。

P3375 【模板】KMP

我们将模式串和匹配串中间加个特殊字符（如 @）连接起来，然后计算 $nxt$ 数组，当发现 $nxt_i=|s_2|$ 时，说明 $S_{0\dots i} $ 的 broder 时 $s_2$，即匹配上了 $s_2$。

#include<bits/stdc++.h>
using namespace std;
int nxt[11451400],j;
string s,t;
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>s>>t;;
    s=t+"@"+s;
	for(int i=1;i<s.size();i++){
		while(s[i]!=s[j]&&j>0)j=nxt[j-1];//失配时迭代
		if(s[i]==s[j])j++;//匹配了
		nxt[i]=j;//记录长度
        if(i>t.size()&&nxt[i]==t.size())cout<<i-2*t.size()+1<<"\n";//输出
	}
    for(int i=0;i<t.size();i++)cout<<nxt[i]<<" ";//输出
	return 0;
}

P4391 [BalticOI 2009] Radio Transmission 无线传输

帮助理解 $nxt$ 数组的好题。

样例字符串为 $\texttt{cabcabca}$。

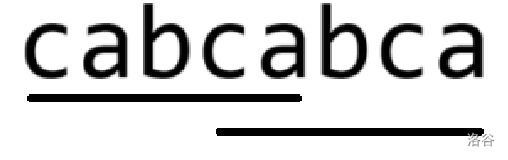
方便观察我们先画出样例的 border 串。

将两串对齐，并以红色串长度均分线段。

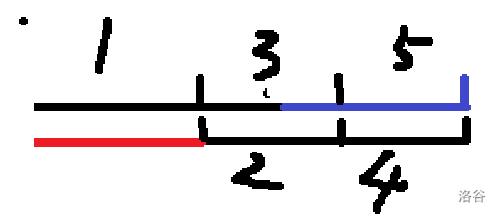
我们发现：

• 1 串等于红色段，因为上下对应。
• 2 串等于 1 串，因为他们是相同前后缀
• 3 串等于 2 串，因为上下对应。
• 4 串等于 3 串，因为他们是公共前后缀。
• ……

红色段是循环节。

而红色段的长度为 $n-nxt_n$，答案就是他。

s=" "+s;
for(int i=2;i<=n;i++){
    while(s[i]!=s[j+1]&&j>0)j=nxt[j];
    if(s[i]==s[j+1])j++;
  	nxt[i]=j;
}
cout<<n-nxt[n];

P9606 [CERC2019] ABB

题目要求的末尾最少要加入字符的数量就是，总长度减去最长回文后缀。

首先解决回文，容易想到将字符串反转，拼在原来的字符串前面或后面。

至于是前还是后呢，我们要求的是最长回文后缀，反转之后，后缀就变成了前缀，所以要拼到前面。

我们记原本的字符串为 $s$，反转后的字符串为 $s'$，拼成的字符串为 $S$。

如果 $t$ 是 $S$ 的一个 border 串，那么说明 $t$ 是回文的，并且是 $s$ 的回文后缀，$s'$ 的回文前缀。

t=s;
reverse(t.begin(),t.end());
s=t+"%"+s;
for(int i=1;i<s.size();i++){
    while(s[i]!=s[j]&&j>0)j=nxt[j-1];
    if(s[i]==s[j])j++;
    nxt[i]=j;
}
cout<<n-nxt[s.size()-1]<<"\n";

习题

• HDU2087
• P4824
• CF25E
• P3435
• P10915
• P1470
• P2375

本蒟蒻第一次写这种文章，如有错误请及时指出。